How in the hell does anyone f— up so bad they get O(n!²)? 🤯 That’s an insanely quickly-growing graph.
Curious what the purpose of that algorithm would have been. 😅
You have two lists of size n. You want to find the permutations of these two lists that minimizes a certain distance function between them.
Surely you could implement this via a sorting algorithm? If you can prove the distance function is a metric and both lists contains elements from the same space under that metric, isn’t the answer to sort both?
It’s essentially the traveling salesman problem
unless the problem space includes all possible functions f , function f must itself have a complexity of at least n to use every number from both lists , else we can ignore some elements of either of the lists , therby lowering the complexity below O(n!²)
if the problem space does include all possible functions f , I feel like it will still be faster complexity wise to find what elements the function is dependant on than to assume it depends on every element , therefore either the problem cannot be solved in O(n!²) or it can be solved quicker
By “certain distance function”, I mean a specific function that forces the problem to be O(n!^2).
But fear not! I have an idea of such function.
So the idea of such function is the hamming distance of a hash (like sha256). The hash is computed iterably by
h[n] = hash(concat(h[n - 1], l[n])).This ensures:
- We can save partial results of the hashing, so we don’t need to iterate through the entire lists for each permutation. Otherwise we would get another factor n in time complexity.
- The cost of computing the hamming distance is O(1).
- Order matters. We can’t cheat and come up with a way to exclude some permutations.
No idea of the practical use of such algorithm. Probably completely useless.
honestly I was very suspicious that you could get away with only calling the hash function once per permutation , but I couldn’t think how to prove one way or another.
so I implemented it, first in python for prototyping then in c++ for longer runs… well only half of it, ie iterating over permutations and computing the hash, but not doing anything with it. unfortunately my implementation is O(n²) anyway, unsure if there is a way to optimize it, whatever. code
as of writing I have results for lists of n ∈ 1 … 13 (13 took 18 minutes, 12 took about 1 minute, cant be bothered to run it for longer) and the number of hashes does not follow n! as your reasoning suggests, but closer to n! ⋅ n.
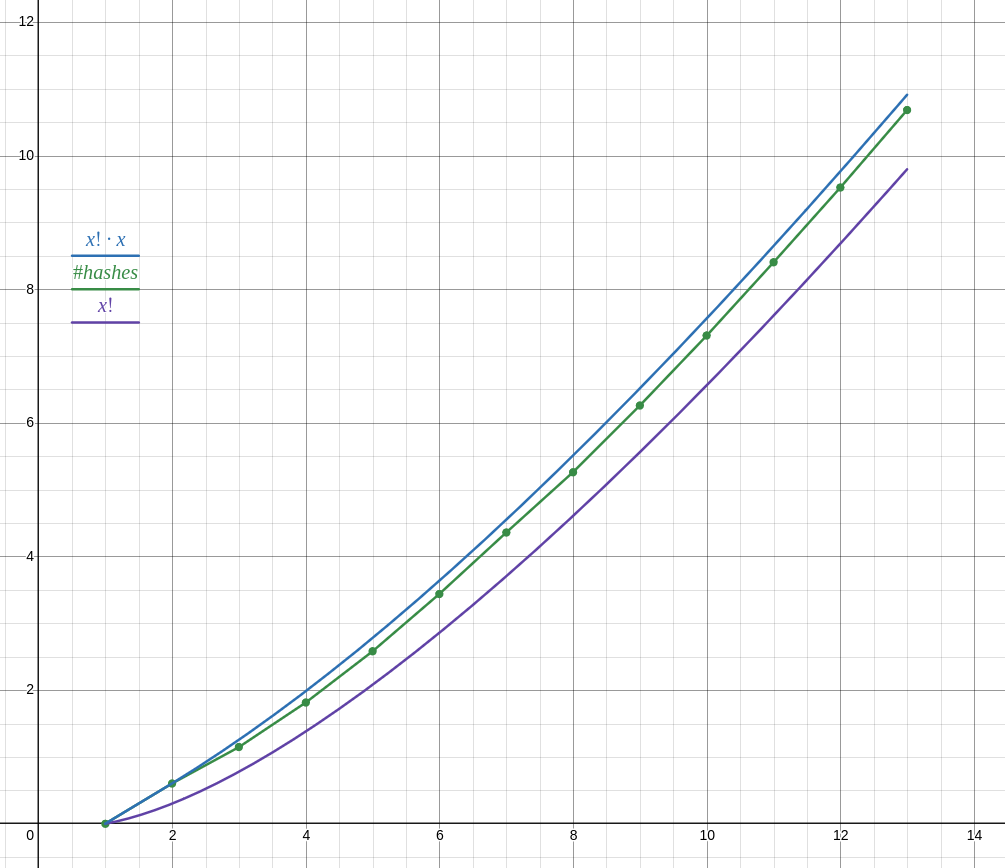
anyway with your proposed function it doesn’t seem to be possible to achieve O(n!²) complexity
also dont be so negative about your own creation. you could write an entire paper about this problem imho and have a problem with your name on it. though I would rather not have to title a paper “complexity of the magic lobster party problem” so yeah
Good effort of actually implementing it. I was pretty confident my solution is correct, but I’m not as confident anymore. I will think about it for a bit more.
So in your code you do the following for each permutation:
for (int i = 0; i<n;i++) {You’re iterating through the entire list for each permutation, which yields an O(n x n!) time complexity. My idea was an attempt to avoid that extra factor n.
I’m not sure how std implements permutations, but the way I want them is:
1 2 3 4 5
1 2 3 5 4
1 2 4 3 5
1 2 4 5 3
1 2 5 3 4
1 2 5 4 3
1 3 2 4 5
etc.
Note that the last 2 numbers change every iteration, third last number change every 2 iterations, fourth last iteration change every 2 x 3 iterations. The first number in this example change every 2 x 3 x 4 iterations.
This gives us an idea how often we need to calculate how often each hash need to be updated. We don’t need to calculate the hash for 1 2 3 between the first and second iteration for example.
The first hash will be updated 5 times. Second hash 5 x 4 times. Third 5 x 4 x 3 times. Fourth 5 x 4 x 3 x 2 times. Fifth 5 x 4 x 3 x 2 x 1 times.
So the time complexity should be the number of times we need to calculate the hash function, which is O(n + n (n - 1) + n (n - 1) (n - 2) + … + n!) = O(n!) times.
EDIT: on a second afterthought, I’m not sure this is a legal simplification. It might be the case that it’s actually O(n x n!), as there are n growing number of terms. But in that case shouldn’t all permutation algorithms be O(n x n!)?
EDIT 2: found this link https://stackoverflow.com/a/39126141
The time complexity can be simplified as O(2.71828 x n!), which makes it O(n!), so it’s a legal simplification! (Although I thought wrong, but I arrived to the correct conclusion)
END EDIT.
We do the same for the second list (for each permission), which makes it O(n!^2).
Finally we do the hamming distance, but this is done between constant length hashes, so it’s going to be constant time O(1) in this context.
Maybe I can try my own implementation once I have access to a proper computer.
you forgot about updating the hashes of items after items which were modified , so while it could be slightly faster than O((n!×n)²) , not by much as my data shows .
in other words , every time you update the first hash you also need to update all the hashes after it , etcetera
so the complexity is O(n×n + n×(n-1)×(n-1)+…+n!×1) , though I dont know how to simplify that
My implementation: https://pastebin.com/3PskMZqz
Results at bottom of file.
I’m taking into account that when I update a hash, all the hashes to the right of it should also be updated.
Number of hashes is about 2.71828 x n! as predicted. The time seems to be proportional to n! as well (n = 12 is about 12 times slower than n = 11, which in turn is about 11 times slower than n = 10).
Interestingly this program turned out to be a fun and inefficient way of calculating the digits of e.
actually all of my effort was wasted since calculating the hamming distance between two lists of n hashes has a complexity of O(n) not O(1) agh
I realized this right after walking away from my devices from this to eat something :(
edit : you can calculate the hamming distance one element at a time just after rehashing that element so nevermind
Scalabe is not always quicker. Quicker is not always scalable.
Let me take a stab at it:
Problem: Given two list of length n, find what elements the two list have in common. (we assume that there are not duplicates within a single list)
Naive solution: For each element in the first list, check if it appears in the second.
Bogo solution: For each permutation of the first list and for each permutation of the second list, check if the first item in each list is the same. If so, report in the output (and make sure to only report it once).
lol, you’d really have to go out of your way in this scenario. First implement a way to get every single permutation of a list, then to ahead with the asinine solution. 😆 But yes, nice one! Your imagination is impressive.
Maybe finding the (n!)²th prime?
this would assume that finding the next prime is a linear operation , which is false
I guess, yeah, that’ll do it. Although that’d probably be yet one or a few extra factors involving n.
if I’m not mistaken , a example of a problem where O(n!²) is the optimal complexity is :
There are n traveling salespeople and n towns . find the path for each salesperson with each salesperson starting out in a unique town , such that the sum d₁ + 2 d₂ + … + n dₙ is minimised, where n is a positive natural number , dᵢ is the distance traveled by salesperson i and i is any natural number in the range 1 to n inclusive .
pre post edit, I realized you can implement a solution in 2(n!) :(
N00b. True pros accomplish O((n^2)!)
Your computer explodes at 4 elements
After all these years I still don’t know how to look at what I’ve coded and tell you a big O math formula for its efficiency.
I don’t even know the words. Like is quadratic worse than polynomial? Or are those two words not legit?
However, I have seen janky performance, used performance tools to examine the problem and then improved things.
I would like to be able to glance at some code and truthfully and accurately and correctly say, “Oh that’s in factorial time,” but it’s just never come up in the blue-collar coding I do, and I can’t afford to spend time on stuff that isn’t necessary.
A quadratic function is just one possible polynomial. They’re also not really related to big-O complexity, where you mostly just care about what the highest exponent is:
O(n^2) vs O(n^3).For most short programs it’s fairly easy to determine the complexity. Just count how many nested loops you have. If there’s no loops, it’s probably
O(1)unless you’re calling other functions that hide the complexity.If there’s one loop that runs N times, it’s
O(n), and if you have a nested loop, it’s likelyO(n^2).You throw out any constant-time portion, so your function’s actual runtime might be the polynomial:
5n^3 + 2n^2 + 6n + 20. But the big-O notation would simply beO(n^3)in that case.I’m simplifying a little, but that’s the overview. I think a lot of people just memorize that certain algorithms have a certain complexity, like binary search being
O(log n)for example.Spot on. Good explanation.
Time complexity is mostly useful in theoretical computer science. In practice it’s rare you need to accurately estimate time complexity. If it’s fast, then it’s fast. If it’s slow, then you should try to make it faster. Often it’s not about optimizing the time complexity to make the code faster.
All you really need to know is:
- Array lookup: O(1)
- Single for loop: O(n)
- Double nested for loop: O(n^2)
- Triple nested for loop: O(n^3)
- Sorting: O(n log n)
There are exceptions, so don’t always follow these rules blindly.
It’s hard to just “accidentally” write code that’s O(n!), so don’t worry about it too much.
lim n->inf t(n) <= O*c, where O is what is inside of big O and c is positive constant.
Basically you can say that time it takes never goes above grapf of some function scaled by constant.
Fun side effect of this is that you can call your O(1) algorithm is O(n!) algorithm and be technically correct.
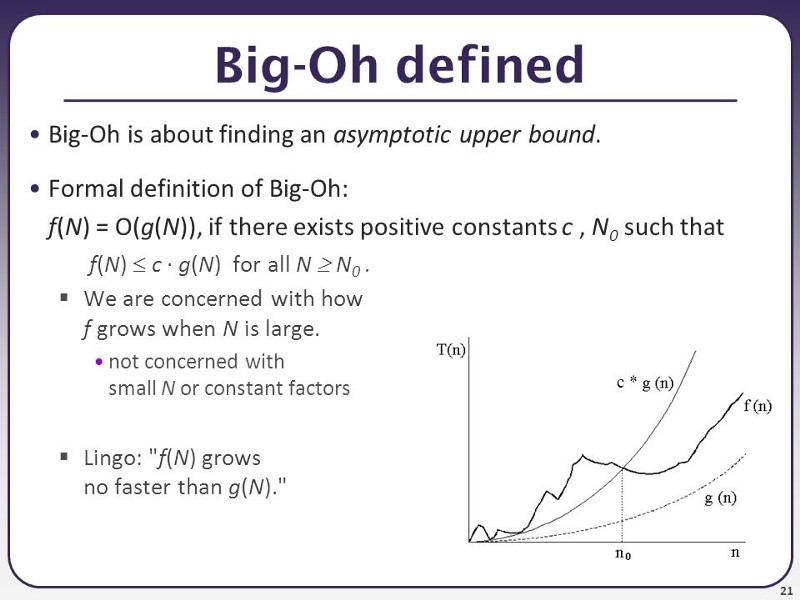
Here is a picture, that may help a little bit. The n is input size, and f(n) is how long does the algorithm runs (i.e how many instructions) it takes to calculate it for input for size n, i.e for finding smallest element in an array, n would be the number of elements in the array. g(n) is then the function you have in O, so if you have O(n^2) algorithm, the g(n) = n^2
Basically, you are looking for how quickly it grows for extreme values of N, while also disregarding constants. The graph representation probably isn’t too useful for figuring the O value, but it can help a little bit with understanding it - you want to find a O function where from one point onward (n0), the f(n) is under the O function all the way into infinity.
Did you write an algorithm to manually drag and drop elements?
Imagine if the algorithm were in Θ(n!²), that would be even worse
You mean omega, not theta
Also constant time is not always the fastest
plot twist to make it worse: you put in in an
onInputhook without even a debounceHow the fuck?!
Oh my god, that’s inefficient as hell.
It may be efficient, not scalable for sure
It has been a while since I have to deal with problem complexities in college, is there even class of problems that would require something like this, or is there a proven upper limit/can this be simplified? I don’t think I’ve ever seen O(n!^k) class of problems.
Hmm, iirc non-deterministic turing machines should be able to solve most problems, but I’m not sure we ever talked about problems that are not NP. Are there such problems? And how is the problem class even called?
Oh, right, you also have EXP and NEXP. But that’s the highest class on wiki, and I can’t find if it’s proven that it’s enough for all problems. Is there a FACT and NFACT class?
For me, my common result would be something like O(shit).
Wait… How can time ever not be constant? Can we stop time?! 😮









